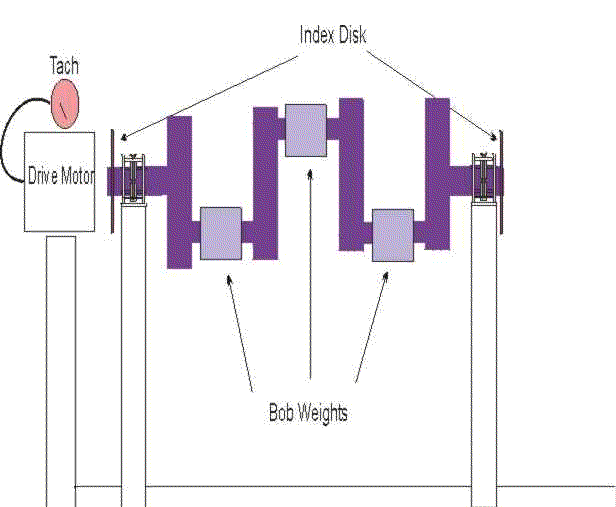
SIDE VIEW
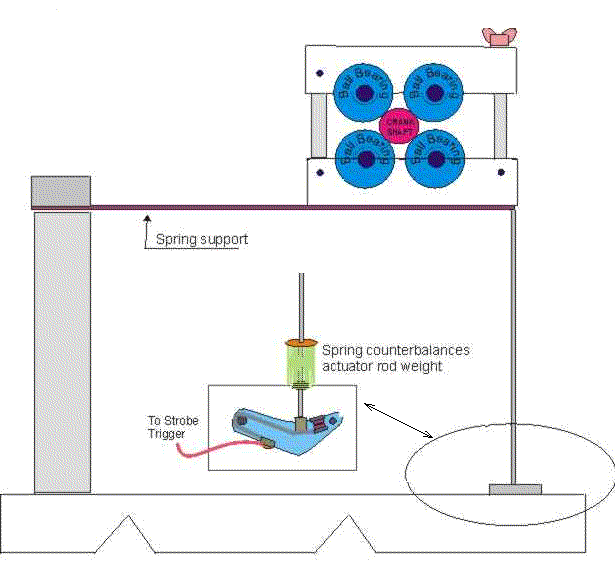
END VIEW
Dale Smith was telling about balancing an engine (on one of the email groups)
and took the time to write up this description with drawings. I have included
it here, thanks to Dale.
I plan to build a machine as described here (Sometime in the future) and will
surely post pictures and details.
All that I know about balancing came from Strictly IC magazine Vol 10 #56.
It discusses balance in relation to small model engines. Very helpful.
Crankshaft Balancing As Best I Recall - by Dale Smith, in the Summer of 2001.
Disclamer: This was from 40 years ago an so my memory may be dusty on the details. However, the principle is where its at so anyone smart enough to balance an engine should be able to tinker it from here with little problem.
The diagrams relate how the old Creitz Speed Shop balancing machine was built. It was welded up from angle and channel stock for a framework with one moveable end support to hold the crankshaft in a horizontal position. The front and rear main journals rested on a pair of ball bearings and were held in place by a clamp arm with two more bearings. I don't recall if the clamp was spring loaded or solid. I think a pretty stiff spring under the wingnut would work just fine.
I also don't recall the exact details of the drive. I seem to have a flat belt on my mind but it may have been some sort of flex coupling. The crankshaft did spin up pretty good but I don't remember the exact RPM.
The bearing blocks were mounted on a pair of leaf springs which, in turn, were mounted on the support uprights. This allowed the the crankshaft to move somewhat in the direction of the heavy spot. In this case, lateral movement was restricted. It could only move up or down by flexing the leaf.
The arrangement in my sketch is upside down but I was too lazy to change it after I found it. As shown, the heavy spot would break the contacts on the bottom side unless your strobelight fired on closing. In that case, the points could be adjusted to make it fire at the top of the revolution.


END VIEW
In any event, the spinning crankshaft will try to jump up and down. The movement is transferred through a linkage rod to an ordinary set of automobile or lawnmower points. The points are connected to fire a strobe light (read that as a timing light) which is pointed at the index wheel, or, what we called a degree wheel since it was marked in degrees.
The firing strobe freezes the image on the index wheel so that the heavy point can be easily read. Even easier if you remembered to add a pointer somewhere along the way.
The crankshaft is stopped and weight is removed from the indicated heavy spot by drilling the counterweight. It can also be added by welding on the light side 180 degrees from the heavy spot. After some weight adjustment, it is spun up again and change in balance noted and corrective measures applied untill there is no indication of imbalance.
Pistons and rods are balanced first on a sensitave pair of scales. Each rod is weighed first and marked. Then each piston is weighed and marked. The lightest piston and rod are chosen and metal is removed (from the heavier ones) to reduce them to the exact weight of the lightest. This is fairly straightforward for pistons but rods get tricky.
Rods are not only balanced for total weight, they are balanced for end weights as well. This is done by suspending one end while the other end rests on the scale and follows the same procedure of matching the lightest.
Once the pistons and rods are matched, a bob weight is calculated as follows: The weight of the big end of the con rod plus half of the weight of the sum of the weight of the small end, piston, pin, and rings.
The weights are made up to the indicated weight and clamped around the rod journals to represent the effects of the pistons and rods being flung up and down by the crankshaft.
| 12973 hits since February 23, 2016 |